L'effet Hall quantique
L’effet Hall quantique est un phénomène relativement récent qui intrigue à la fois les expérimentateurs et les théoriciens. L’apparition de plateaux situés à des fractions rationnelles (de dénominateurs impairs), avec une très grande précision (de l’ordre de $10^{-7}$ pour certaines valeurs) dans la courbe reliant la conductivité (transverse) au champ magnétique a surpris les théoriciens (voir figure plus bas). Aujourd’hui, une vingtaine d’années après les premières expériences, de nombreuses suggestions ont été faites pour expliquer ces courbes. Cependant, malgré d’énormes succès, une théorie expliquant toutes les facettes de ce phénomène n’a pu encore être construite.
Mes travaux sur l’effet Hall quantique peuvent être regroupés en trois grands axes, correspondant à trois approches distinctes que j’ai entreprises avec mes collaborateurs. La seconde de ces approches, dénommée ici “Théories effectives”, s’applique en réalité à une plus large classe de problèmes que l’effet Hall quantique lui-même.
Les motivations de ces recherches sont exposées dans le texte qui suit, les articles décrivant ces travaux sont disponibles sur la page de mes publications.
Phénoménologie de l’Effet Hall
Il s’agit de travaux de recherche au niveau phénoménologique, qui ont pour but de comprendre et décrire les structures apparentes dans les hiérarchies des états de Hall.
En effet, d’un point de vue purement expérimental, certaines structures sont apparues dans les états de Hall et les états métalliques, qu’on a appelé “hiérarchies”. La constatation est que certains états n’apparaissent dans une expérience particulière que si d’autres états “parents” sont eux aussi présents. Il existe donc une hiérarchie entre les états.
Deux grandes propositions ont été faites pour décrire ces hiérarchies. Jain a proposé une hiérarchie basée sur le choix d’un état métallique (état dont le facteur de remplissage est à dénominateur pair), dont des états de Hall (état dont le facteur de remplissage est à dénominateur impair et présentant un plateau typique) sont les “enfants”. D’autre part, Haldane et Halperin ont proposé une hiérarchie plus profonde (dans le nombre de niveaux), où à chaque niveau un état de Hall “parent” chapeaute une infinité d’états de Hall “enfants”. Cette hiérarchie repose sur les fractions continues.
Des propositions de classifications et de reproductions de ces hiérarchies ont été alors proposées, souvent basées sur l’utilisation des groupes modulaires (sous-groupes de $SL(2,\mathbb{Z})$), car ce sont des groupes naturels qui agissent sur les fractions.
Mon implication dans ce domaine de recherche fait suite à des travaux de Y. Georgelin et J.-C. Wallet sur une proposition d’utiliser le groupe modulaire $\Gamma(2)$ pour reproduire et généraliser les hiérarchies de Jain. Etant donné un état métallique, on lui associe les orbites de $1$ et $0$ par l’action du sous groupe de $\Gamma(2)$ laissant cet état métallique invariant. On obtient ainsi les états de Hall “enfants” de cet état métallique.
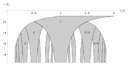
En collaboration avec Y. Georgelin et J.-C. Wallet, nous avons montré que l’information donnée par cette démarche pouvait complètement être encodées dans des diagrammes, appelés diagrammes de visibilité. Ces diagrammes contiennent toutes les généralisations des hiérarchies de Jain mentionnées ci-dessus obtenue à partir de $\Gamma(2)$. Une étude mathématique de ces diagrammes a été esquissée dans cet article. De plus, une information nouvelle sur les largeurs des plateaux des états de Hall a été proposée et confrontée avec succès aux courbes expérimentales.
Nous avons aussi montré comment l’action du groupe modulaire $\Gamma(2)$ sur les états de Hall pouvait contraindre la fonction $\beta$ (modulo l’hypothèse relativement naturelle que cette fonction est holomorphe) dont le flot du groupe de renormalisation est celui associé aux transitions entre états de Hall.
Par la suite, nous avons montré comment la construction du diagramme de visibilité évoqué ci-dessus pouvait donner lieu à deux autres diagrammes de visibilité. Ces deux autres diagrammes encodent cette fois entièrement les hiérarchies de Haldane et Halperin, et complètent donc de façon satisfaisante l’ordonnancement de tous les états métalliques et de Hall empiriquement décrit à partir de l’expérience. De plus, ces diagrammes pouvent être rapportés à des données expérimentales précises : d’une part des bandes explicitement observées dans le plan “champ magnétique”—“tension de porte” (nombre de porteurs de charges dans l’expérience), et d’autre part le diagramme des phases de l’effet Hall.
Il s’ensuit qu’un grand nombre de propriétés globales de l’effet Hall quantique sont complètement contenues dans ces diagrammes de visibilité : les hiérarchies proposées dans la littérature jusqu’à présent, le diagramme des phases, les largeurs relatives des plateaux. Une conséquence de ces travaux est que les groupes modulaires ne sont sûrement pas suffisants pour reproduire cet ensemble d’informations.
Les diagrammes de visibilités sont donnés par les images ci-dessous, ainsi qu’une image observée des bandes. Les diagrammes des phases expérimental et prédit ont même structure globale.
Théories effectives
Le second grand axe de recherche mené dans ce cadre prend pour point de départ les théories des champs phénoménologiques applicables à l’effet Hall. Il s’agit de mettre en place des théories effectives répondant au cahier des charges étroit des propriétés requises pour décrire les états de Hall et les transitions entre états. De même, il serait souhaitable de pouvoir en déduire, par des propriétés de symétrie, les hiérarchies de ces états, tels qu’ils ont été rappelés ci-dessus.
Des propositions de telles théories effectives ont été réalisées en utilisant des théories des champs de type Chern-Simons. Une classe de modèles effectifs en $(2+1)$ dimensions basés sur un lagrangien de type Maxwell-Chern-Simons pour la dynamique du champ de jauge et d’un couplage non minimal des champs de jauge au champs de matière a été étudié. L’intérêt d’un tel modèle est que le terme de type Maxwell introduit une non localité qui rend compte du fait que le système est un système en $(3+1)$ dimensions contraint à un plan. Nous avons montré que cette classe de modèle renferme une symétrie de dualité cachée (action de $\mathbb{Z}_2$), que nous illustrons dans un modèle effectif décrivant la dynamique de vortex massifs chargés en interaction.
Par la suite, ce type de modèle a été couplé au fond uniforme d’un champs chargé. Il est alors possible de montrer que certains de ces lagrangiens pouvaient donner lieu à des configurations d’énergie minimale statique à symétrie sphérique. Certaines de ces solutions sont numériquement étudiées dans ces travaux.
Nous avons alors appliqué ces techniques à une situation expérimentale qui se révèle être semblable à celle de l’effet Hall : les condensats de Bose en rotation rapide. Nous nous sommes intéressés plus particulièrement aux propriétés de stabilisation de gaz de Bose attractifs en rotation très rapide. Nous avons comparé cette propriété spécifique entre les modèles de type Chern-Simons et ceux de type Maxwell-Chern-Simons avec terme de couplage non minimal. Nous avons compris que la stabilité peut toujours être obtenue pour les premiers types de modèles, alors qu’elle requiert que la portée de l’interaction du champs de jauge statistique soit inférieure à la longueur d’onde type des atomes dans le second cas.
il est aussi possible d’utiliser un modèle de type Chern-Simons-Landau-Ginzburg lié aux hiérarchies de bosons composites pour décrire des états fractionnaires de Hall dans les gaz de bosons piégés dans un potentiel harmonique $2D$ en rotation rapide. Une prédiction de ces travaux est que les valeurs possibles de $\nu = p/q$ (rapport entre le nombre de particules et le nombre de vortex), pour ces états, correspondent à la contrainte $pq$ pair. Cette prédiction est compatible avec des simulations numériques précédemment effectuées par d’autres auteurs.
L’Effet Hall par les principes de la mécanique quantique
Le troisième axe de recherche que nous avons développé concernant l’effet Hall quantique se base sur les principes de la mécanique quantique.
Précédemment, des auteurs avaient montré qu’il était possible de déduire certaines propriétés de l’effet Hall quantique à partir du problème de Landau (particules chargés dans un champs magnétique constant). Ces différentes approches reposaient sur des géométries sous-jacentes différentes, et quelques points importants en avaient été déduits :
- Dans cette approche, la conductance de Hall, peut être reliée, via la formule de Kubo, à une expression intégro-différentiable très semblable au calcul de la première classe de Chern dans la théorie des fibrés (ici un fibré de groupe de structure $U(1)$).
- La géométrie choisie joue un rôle important pour interpréter la conductance de Hall sous cette forme comme une vraie classe caractéristique, et montrer ainsi qu’elle ne peut prendre que des valeurs entières.
L’un des points faibles les plus importants de ces approches est que la conductance de Hall devait être entière (puisque interprétée comme une classe caractéristique). Ces modèles ne pouvaient donc pas s’appliquer à l’effet Hall quantique dans sa généralité, puisque des valeurs fractionnaires de la conductance de Hall y apparaissent…
En collaboration avec F. Chandelier, Y. Georgelin et J.-C. Wallet, nous avons revisité cette approche, en insistant dès le départ sur l’importance de la géométrie de l’expérience.
En effet, l’expérience de Hall est très particulière au sens suivant. L’échantillon est un domaine borné plan, dans lequel les lois de la mécanique quantique sont applicables (l’expérience est réalisée dans ce but, par un refroidissement extrême afin de préserver les propriétés quantiques). Dans ce domaine plan, nous avons donc affaire à un problème (quantique) de Landau tout à fait “ordinaire”. Cependant, afin de mesurer l’intensité et la tension (cette dernière n’étant in fine que la mesure déguisée d’une intensité), des fils sont reliés aux quatre bords de ce domaine, formant ainsi deux boucles de courant reliant les bords opposés de l’échantillon (ceci constitue déjà en soi une approximation de la géométrie, mais pas des principes sous-jacents qui la gouvernent). Dans ces fils, des courant ordinaires, sujets aux lois classiques, circulent (les appareils de mesures sont “classiques” au sens où on l’entend en mécanique quantique).
C’est à partir de ces considérations que nous avons défini le modèle que nous avons étudié. Mathématiquement, il correspond au problème bien connu de l’extension autoadjointe d’opérateurs symétriques sur un domaine plan (l’opérateur hamiltonien, les deux opérateurs impulsions avec couplage minimal au champs magnétique constant dans les deux directions d’espace), avec ici des conditions aux bords de nature intégro-différentiable : ce sont en effet des conditions écrites à partir de la conservation des courants entrant et sortant aux quatre bords du domaine.
Nous avons mené une étude très complète de ce modèle, et nous avons pu, dans un cas spécifique où une géométrie émergeante est particulièrement simple, calculer explicitement la conductance de Hall à partir de ces principes. Ce calcul n’avait jamais été réalisé jusqu’au bout dans de telles approches. Par la suite, nous avons étendu cette étude à des situations où la géométrie émergeante était moins simple.
Un bref résumé de quelques lignes de ce que nous avons découvert en menant ces recherches s’impose. Le champs magnétique constant $B$ est un paramètre de définition du domaine d’extension autoadjointe des opérateurs considérés. Mais il n’est pas le seul, et nous avons exhibé deux autres paramètres angulaires, appelés $\gamma$ et $\eta$, définis tous les deux sur $[0,2\pi[$. Par analogie avec les fonctions de Bloch, nous avons appelé l’espace de ces paramètres l’“espace réciproque”, l’espace direct étant celui de l’échantillon “réel”. Le champ magnétique indexe la géométrie d’un fibré dans l’espace direct (la géométrie émergeante évoquée plus haut) :
- dans le cas où il est entier, le champ magnétique s’identifie à une première classe de Chern d’un fibré en droites complexes sur un tore (l’échantillon dont on a identifié les bords opposés) ;
- dans le cas où il est rationnel, il définit un fibré sur une surface orientable poncturée obtenue par recollements de copies (virtuelles) de l’échantillon ;
- dans le cas irrationnel, aucune géométrie ordinaire ne peut lui être associé.
Quant à la conductance de Hall, grâce à la formule de Kubo évoquée plus haut, elle s’identifie dans certaines situations (dépendant de $B$) à une classe caractéristique d’un fibré construit sur une surface obtenue par recollements de copies virtuelles de l’espace réciproque.
Ainsi, il existe deux géométries dans ce contexte : la géométrie directe, gouvernée par $B$, et la géométrie réciproque, gouvernée par la conductance de Hall. Ces deux géométries sont reliées entre elle par une symétrie que nous avons exhibée, et qui se ramène à l’action du tore non commutatif sur l’espace des fonctions d’ondes. Faire varier $B$ dans l’espace direct revient à changer la géométrie associée, qui, à travers cette symétrie, modifie à son tour la géométrie dans l’espace réciproque, et donc la valeur de la conductance de Hall.
Les cas où nous sommes parvenus à calculer explicitement la conductance de Hall par cette démarche correspondent à des géométries dans l’espace direct pour laquelle $NB$ est entier, où $N$ est le nombre de porteurs de charges. Le point important de notre résultat est que la conductance de Hall est intrinsèquement fractionnaire dans ce calcul, car elle ne correspond pas exactement à la valeur de la première classe de Chern sur un fibré en droites : en effet, c’est seulement un certain multiple de cette conductance qui s’identifie à une telle classe de Chern ! Par la suite, nous avons traité le cas où $NB$ est fractionnaire, et caractérisé complètement la géométrie émergeante correspondante.
Des développements mathématiques consécutifs à ces considérations font l’objet de recherches actuelles. Il agit de reconsidérer et de généraliser cette problématique dans un cadre qui permette l’accès aux situations géométriques moins simples, pour les cas où $B$ est irrationnel, qu’il semble impossible de traiter par des considérations de géométrie ordinaire. Cette nouvelle approche requiert donc l’usage d’objets mathématiques issus de la géométrie non commutative, où la symétrie du tore non commutatif jouera sans aucun doute un rôle prépondérant.